Talking about DAB and talking about DRM means talking about Digital Radio. Of course the radio signals themselves are still analog, it is the content that is digital. The advantage of having digital content is obvious, anything that can be expressed as a sequence of bits - audio, video, pictures, websites etc etc - can be transmitted. In DAB, Digital Audio Broadcasting, audio services carry usually text, pictures and sometimes complete websites with them.
The downside is of course that the receiver is (far) more complex than that for e.g. AM or FM. Listening to digital radio with a crystal receiver, or an old fashioned receiver with glowing tubes does not make much sense then: radio technique is changing.
On the receiving side we have to do things on two levels. First of all we have to convert an analog signal into bits and second, we have to interpret the bits and (re)construct the audio or multimedia that was input to the transmitter.
There are a few different approaches for the implementing digital radio. Different parts of the world use different systems. Europe and Australia have embraced the afore mentioned DAB (Digital Audio Broadcasting) (or better DAB+), some African and Asian countries experiment - and implement - DRM, Digital Radio Mondiale, while the US have their own system.
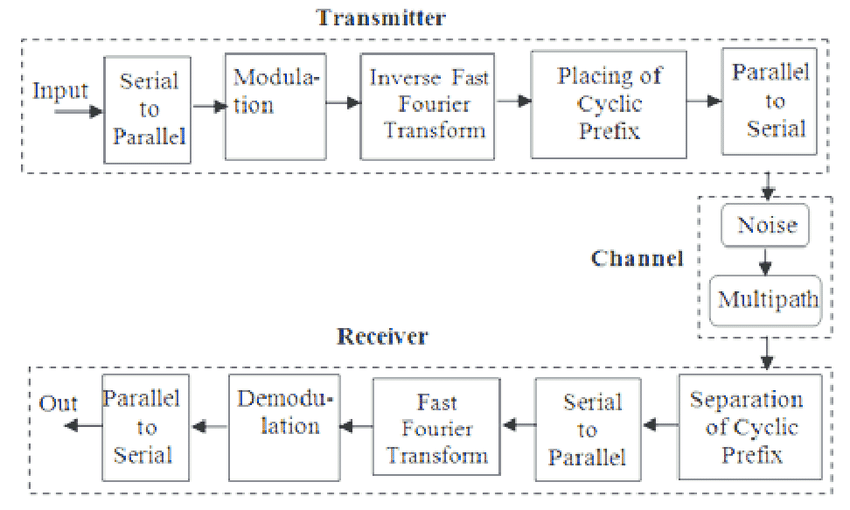
Most systems for digital radio share a single underlying principle for the transmitting of bits. The principle is based on OFDM, Orthogonal Frequency Division Modulation. While that sounds complicated, it is - at least in principle - simple.
We start with a vector of digital data (encoded as complex numbers). We consider the data elements to be "carriers", i.e. elements in the frequency domain. We apply an inverse FFT operation on these carriers. As known, applying an inverse FFT operation to elements in the frequency domain creates the FFT-ed elements in the time domain. (It is common to extend the input vector are both sides by a number of null carriers.)
To add redundancy, each vector resulting from the inverse FFT operation is extended (preceded) by a so called cyclic prefix. This prefix consists of copies of the last N elements of the vector. The function of the cyclic prefix is twofold:
it can be used to decide where in the time domain the word starts, correlating the values in the prefix with the last samples of the word is the technique to apply here;
By looking at the phase difference between corresponding elements in the cyclic prefix and the last segment of the word gives a (good) indication of the frequency offset.
So, as an example, if we start with a vector of say 1536 complex values, i.e. the initial carriers for a DAB word, we extend the vector to 2048 carriers by adding 256 null carriers to each side of the vector. The FFT operation generates a vector of 2048 time domain elements. We make a copy of the last 504 elements of output of the FFT operation and put that in fromt of the vector of 2048 elements resulting in a vector of 2552 elements.
The values in the extended vector, in this example 2552 complex values, are then fed into an DA converter, the result of which is mixed with an oscillator signal to shift the frequency. The resulting analog signal is amplified and fed into some antenna system.

A receiver for digital radio takes the reverse route. We assume we have a device that is able to tune to a given frequency, shift the signal frequency to an IF of 0, and feed the signal to an AD converter. The software at the receiver side then collects the samples, in the example above 2552 samples per group, removes the cyclic prefix, feeds the vector - in the example now 2048 complex values - into an FFT processor, and takes from the result the 1536 carriers by removing the null carriers. The result then is the basis for extracting bits and interpreting the signal.
There are some details though that need some attention at the receiver side. The transmitter sends blocks of data, and on the receiver side we need to figure out where such block can be found in this samplestream. In most cases, we make use of the aforementioned cyclic prefix. Since the prefix elements are copies of elements at the end of the vector, we apply correlation to detect the start. As soon as the correlation between a sequence of elements with length of cyclic prefix with a sequence of elements furtheron is maximal, we "know" where the data in the block is starting.
Once we can identify the start of blocks in the incoming sample stream, we collect a vector of elements and apply an FFT transform to get carriers back.
One of the drawbacks of the OFDM approach is the sensitivity to frequency errors. Consider the case of a frequency error in the incoming data stream. If the offset of the frequency is sufficiently large, the carriers, resulting from the FFT operation are just wrong. It might be the case that the value found as value of carrier i is axrually the value for carrier i + 1. Such as error makes it obviously impossible to extract the right bits.
In the front end part of a receiver for digital radio, lots of attention is (to be) paid to synchronization, both time and frequency.
Of course, the the value of the carriers obtained from the FFT operation is modified by the transmission channel. Both amplitude and phase can be altered by the transmission. Therefore, quite some processing might have to be done in the actual extraction of bits. How this is done depends on the type of digital radio.
As an example, DRM requires for decoding that the values are a true copy (the phase and the amplitude) of the values that were traansmitted. Of course the transmitter has to add elements to the signal to make that possible.
In DAB a different approach is taken. Bits are encoded as phase difference betweem corresponding carriers in subsequent words.
Of course, techniques such as viterbi encoding, reed solomon coding and adding CRC's to segments of code can be - and are - used to add sufficient redundancy to the transmission to allow a decoder to extract the bits, recover from and repair errors and generate the desired output.